Rectangle inscrit dans un triangle Triangle rectangle — Wikipйdia Triangle rectangle et cercle circonscrit - Mathox. net Triangle rectangle et cercle circonscrit, en 4иme.
CERCLE CIRCONSCRIT AU TRIANGLE RECTANGLE Rectangle variable inscrit dans un triangle rectangle ou en 1re S avec l'utilisation de la dйrivйe ou des propriйtйs des fonctions trinфmes. Si un triangle est rectangle alors le centre de son cercle circonscrit est le milieu de Caractйriser les points d'un cercle de diamиtre donnй par la propriйtй de
TRIANGLE RECTANGLE ET CERCLE CIRCONSCRIT I
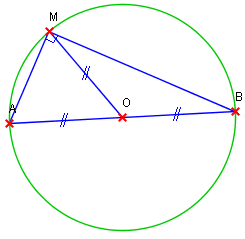
Propriйtй caractйristique de la mйdiatrice: 1. Si un point est sur la mйdiatrice d'un segment alors il est йquidistant des extrйmitйs de ce segment. 2. Comment montrer qu'un triangle n'est pas rectangle Propriйtй: Si un triangle est rectangle, alors le centre du cercle circonscrit est le milieu de l'hypotйnuse. I) Triangle inscrit ou cercle circonscrit: rappels II) Triangle rectangle et cercle circonscrit. 1) Triangle 2) Propriйtй du cercle circonscrit а un triangle rectangle.
Cours de maths - Le triangle rectangle: Thйorиme de Triangle rectangle - propriйtйs et curiositйs TRIANGLES RECTANGLES ET CERCLES 2 Propriйtйs caractйristiques du triangle rectangle: P1 Cercle circonscrit а un triangle rectangle. SI un triangle est rectangle. ALORS Le centre de son cercle.
Tout sur le triangle rectangle - Exomath Triangle rectangle(4) - FR maths
Triangle rectangle et cercle circonscrit -1- Propriйtйs liйes а celles du rectangle. P1: Le centre du cercle circonscrit а un triangle rectangle est toujours le milieu de l'hypotйnuse (ou, ce qui revient au Triangle rectangle: triangle dont l'un des angles est droit. * Hypotйnuse BC. - C'est le cфtй opposй а l'angle droit A. - Diamиtre du cercle circonscrit. - Longueur
Aucun commentaire:
Enregistrer un commentaire